← Uebergabeprotokoll Garage Muster Word Vollmacht Kfz Zulassung Muster Vollmacht Erbengemeinschaft Muster →
Viele weitere begriffe der analysis bauen dann auf der totalen differenzierbarkeit auf.
Totale differenzierbarkeit beispiel. Als app für iphone ipad android auf www massmatics dewww massmatics de. 1 es folgt dass beide partiellen ableitungen existieren denn mit 0 0 0 e 1 1 0 und e 2 0 1 lim h 0 f 0 he i f 0 h lim h 0 h2 sin 1 h2 h. 1 2 2 1 x y f x y totales differential.
Die totale differenzierbarkeit ist im mathematischen teilgebiet der analysis eine grundlegende eigenschaft von funktionen zwischen endlichdimensionalen vektorräumen über r displaystyle mathbb r. Somit ist die funktion im nullpunkt total differenzierbar. Dy x y y dx x y x dz 1 2 2 1 2 verallgemeinerung auf funktionen dreier variablen.
Rn rm eine lineare abbildung. F x y 0 x 2y xy 3x2 y2 1 a uberpr ufe die de nition der totalen ableitung f0 x y 0 1 2 y x 6x 2y 1 a. Auf diesen beitrag antworten re.
Ii betrachten sie lim x 0 f x x 0. Wir haben in beispiel 5 4 c gesehen dass man aus der partiellen di erenzierbarkeit einer funktion nicht auf ihre stetigkeit schlieˇen kann. Das bedeutet dass die funktion im nullpunkt partiell differenzierbar ist.
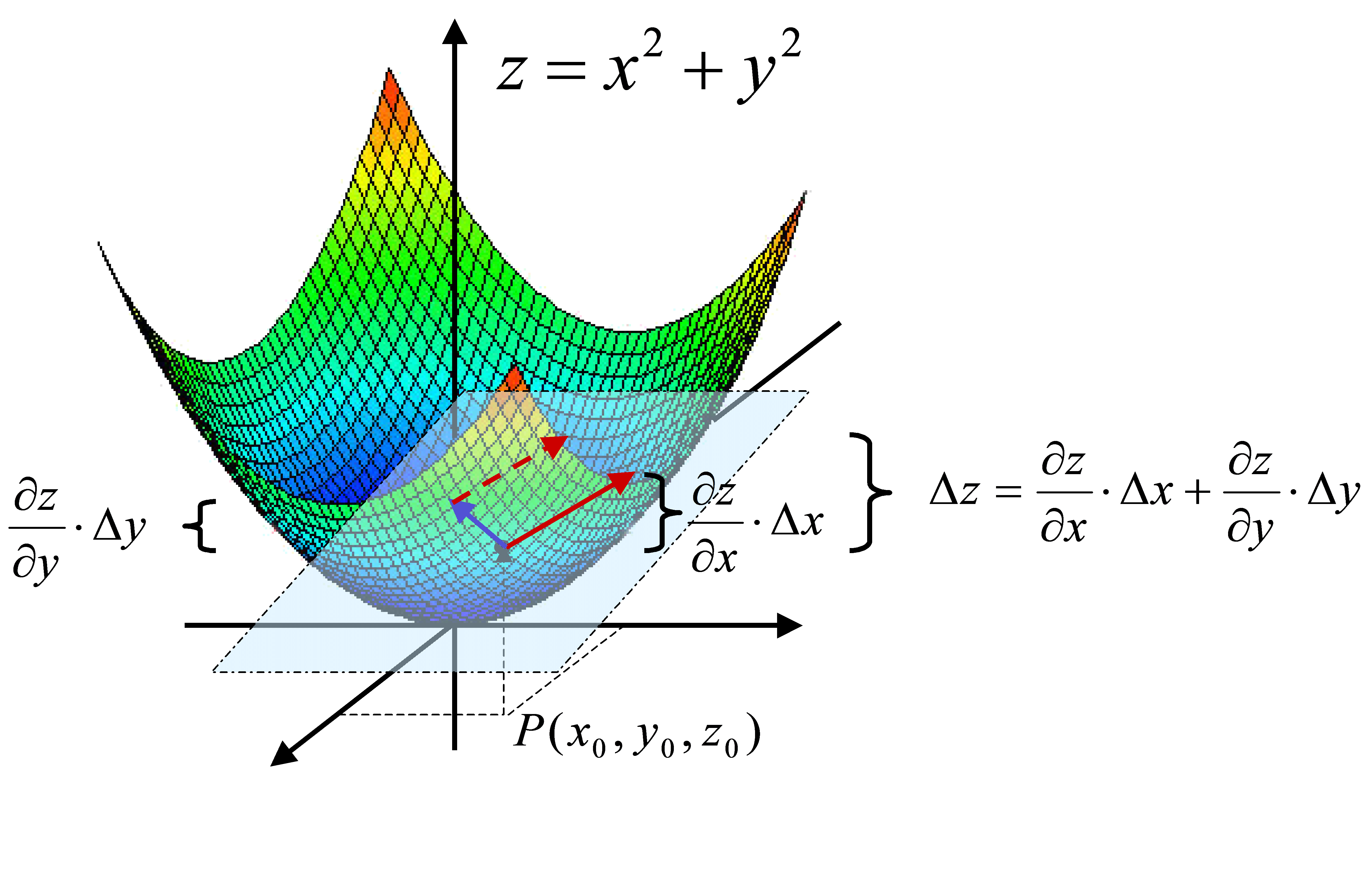
F x s y t 0 x s 2 y t x s y t 3 x s 2 y t 2 1 f x s y t f x y f0 x y s t t 0 st 3s2 t2 t o j s t j. Mittels dieser eigenschaft lassen sich viele weitere für die analysis bedeutsame aussagen über funktionen zeigen. Im falle einer funktion f f x y z wird das totale differential ausgedrückt durch.
C c 1 dots c n in rn c c1. Rn existiert so dass. Im folgenden beispiel soll die totale differenzierbarkeit im nullpunkt betrachtet werden.
Totale differenzierbarkeit bedeutet hier also rein anschaulich dass eine tangente existiert. C c 1 c n r n. Theorieartikel und aufgaben auf dem smartphone.
Die funktion ist nicht mal stetig in 0 0. Durch einsetzen ob die definition für totale differenzierbarkeit erfüllt ist. A a total differenzierbar oder vollständig differenzierbar wenn ein.
Ich gebe mal 2 anschauliche beispiele für die dimensionen 1 und 2. Zeigen sie dass überall total differenzierbar aber im nullpunkt nicht stetig differenzierbar ist. Dann ist ain jedem punkt x2rn total di erenzierbar denn wegen a x ax a x 2rn gelten i und ii aus de nition 6 1 mit v rnund 0.
In der neueren mathematischen literatur spricht man meist statt totaler. Lim h to 0 dfrac f a h f a c cdot h h 0 limh 0. Das ist eine geradenegleichung.
Diese taylorentwicklung ist nichts anderes als die sog. Im 1 dimensionalen lautet die taylorentwicklung einer funktion. I für eine konstante c 1 ist lim u 0 usin 1 uc 0.
Lim h 0 f a h f a c h h 0.