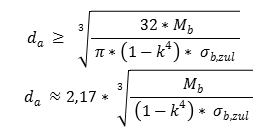← Vorlage Kfz Ueberlassungsvereinbarung Privat Wertgarantie Kuendigen Vorlage Word Vorlage Geburtstag Glückwunsch →
Dies ist das drehmoment die berechnung der spannung und verformung erfolgt in den nächsten schritten.
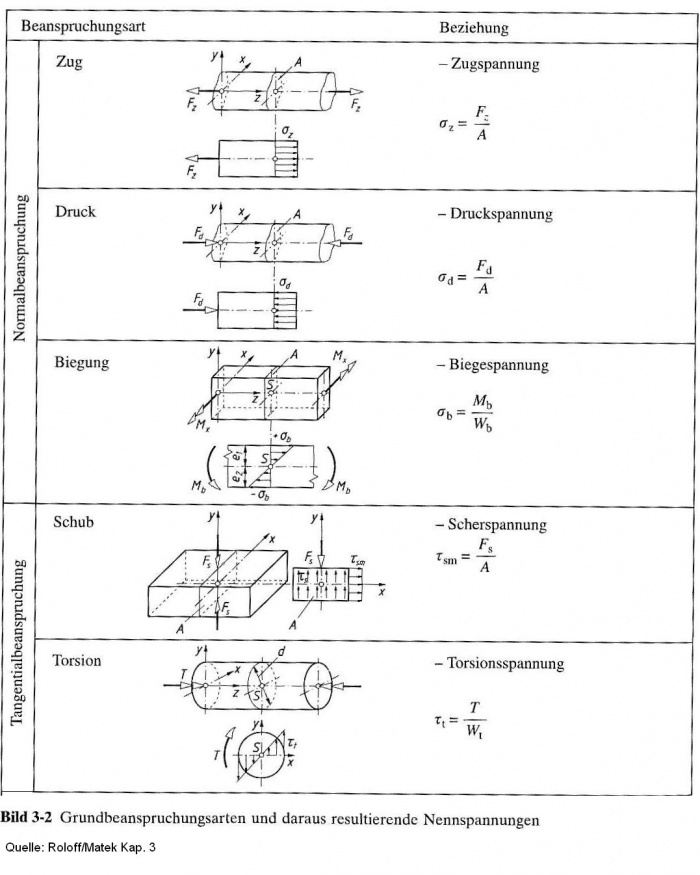
Torsionsmoment berechnen beispiel. A berechnen sie die querschnittswerte i y i z und i yz. Am punkt 1 ist m b 1 m a da hier das moment m a angreift. 2 2 2 2 k ed ef k k ed ed ef k d t b b t τ t d τ folgt die schubspannung.
Schräge kanten und ab rundungen werden nicht berück sichtigt. Zumeist liegt eine überlagerung mit biegemomenten und querkräften vor. Eine reine torsion ist selten.
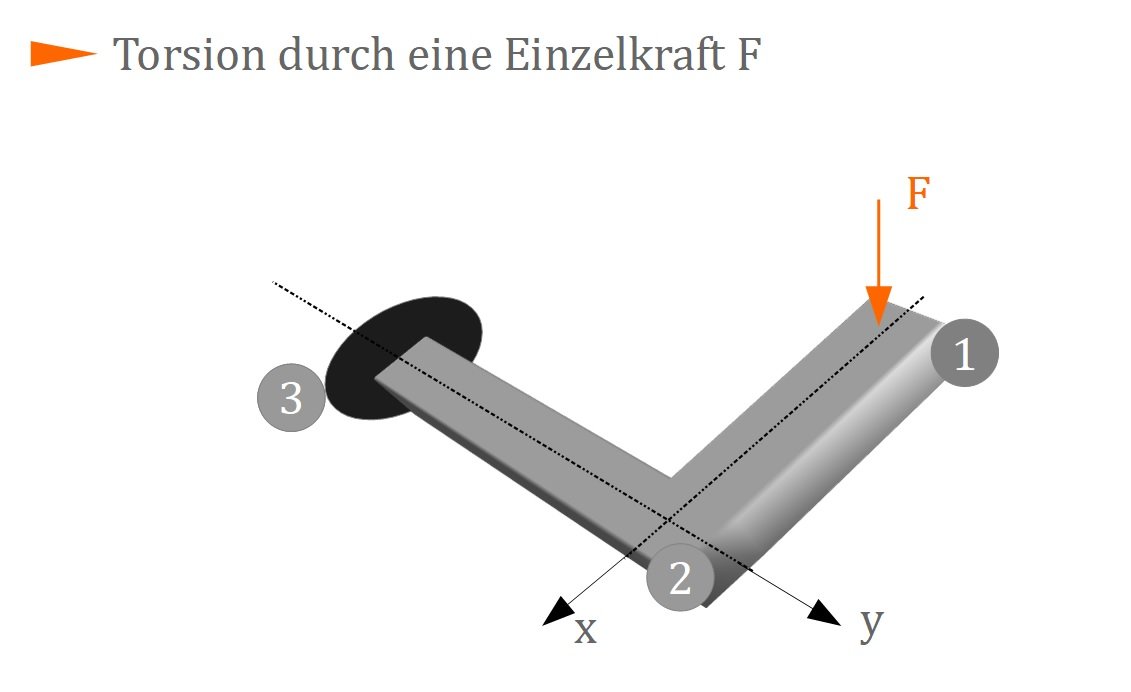
Durch eine feste ein spannung an einem ende ent stehen zusätz liche normal spannungen die unter um ständen nicht ver nach. In der nächsten abbildung siehst du hierzu unterschiedliche fälle für das auftreten einer torsion. A k b k d k 2 1 3 kernumfang.
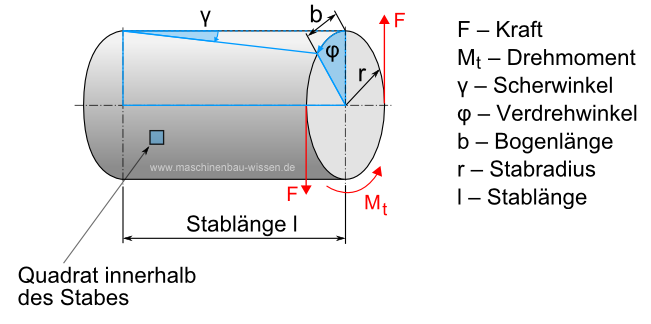
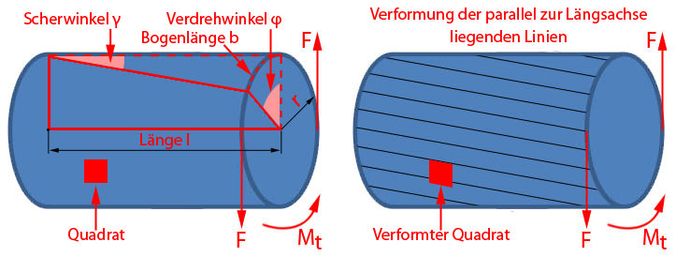
Das hexagonale stabprofil wird durch ein torsionsmoment m t belastet. Begin alignat 2 tau zul 60 mathrm n mm 2 quad m t 150 mathrm nm t 3 mathrm mm quad end alignat ges. M t torsionsmoment f kraft r hebelarm stabradius.
K 2 1 4 mit dem torsionsmoment. Eine torsion tritt in bauteilen immer dann auf wenn kräfte momente oder kräftepaare wirken deren wirkungslinie nicht in der balkenachse oder trägheitsebene liegen. Das torsionsmoment ist so die kraft die bei dem körper die verdrillung auslöst.
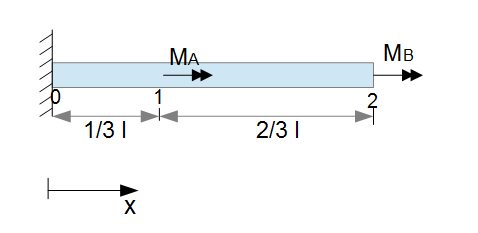
Am stabende 2 ist m b frac 1 3 m a. 4 2 beispiele das torsionsmoment ist in jedem querschnitt gleich und hat den wert mx. Die größte schubspannung tritt im abschnitt cd auf.
Die maximale schubspannung tritt dort auf wo das torsionsmoment am größten ist. Wt cd 1 2 πr0 3 τmax mx wt cd 2mx πr0 3. Am beispiel rechteckquerschnitt siehe bild oben ergibt sich.
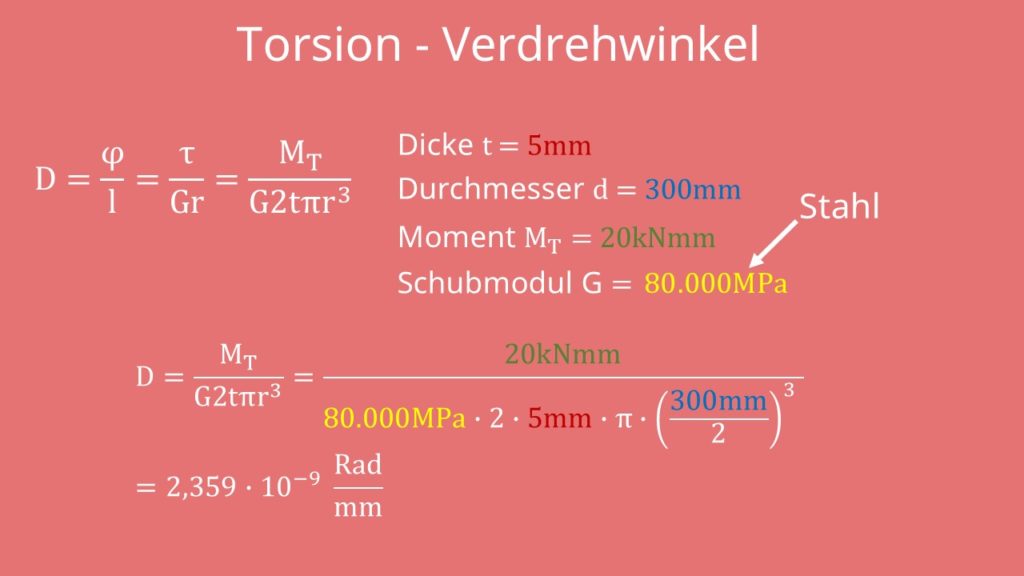
Diesen zusammenhang in eine mathematische formel übersetzt ergibt. B bestimmen sie die querkraft q z. Hinweise die berechnung der quer schnitts fläche a und des torsions wider stand moments w t erfolgt für idealisierte profile.
Ef ed k ef ed ed a t t t ν τ 2 mit k ed ed a t 2 ν in kn m 2 1 5 τ. Wir erhalten das torsionsmoment m t indem wir die kraft f mit länge r des eingesetzten hebels multiplizieren. Querkraft und torsion 8 pkt.
Die momentenlinie liegt demnach im negativen bereich. Mit dem torsionswiderstandsmoment gilt. Am stabende ist m b also frac 1 3 m a.
Wird die verwölbung des trägers ver hindert z. Jede seite hat die dicke t.