← 3d Buchstaben Vorlagen Anmeldung Kindergarten Vorlage Annonce Schreiben Muster →
Vor 6 monaten hatte er einen hirninfarkt erlitten.
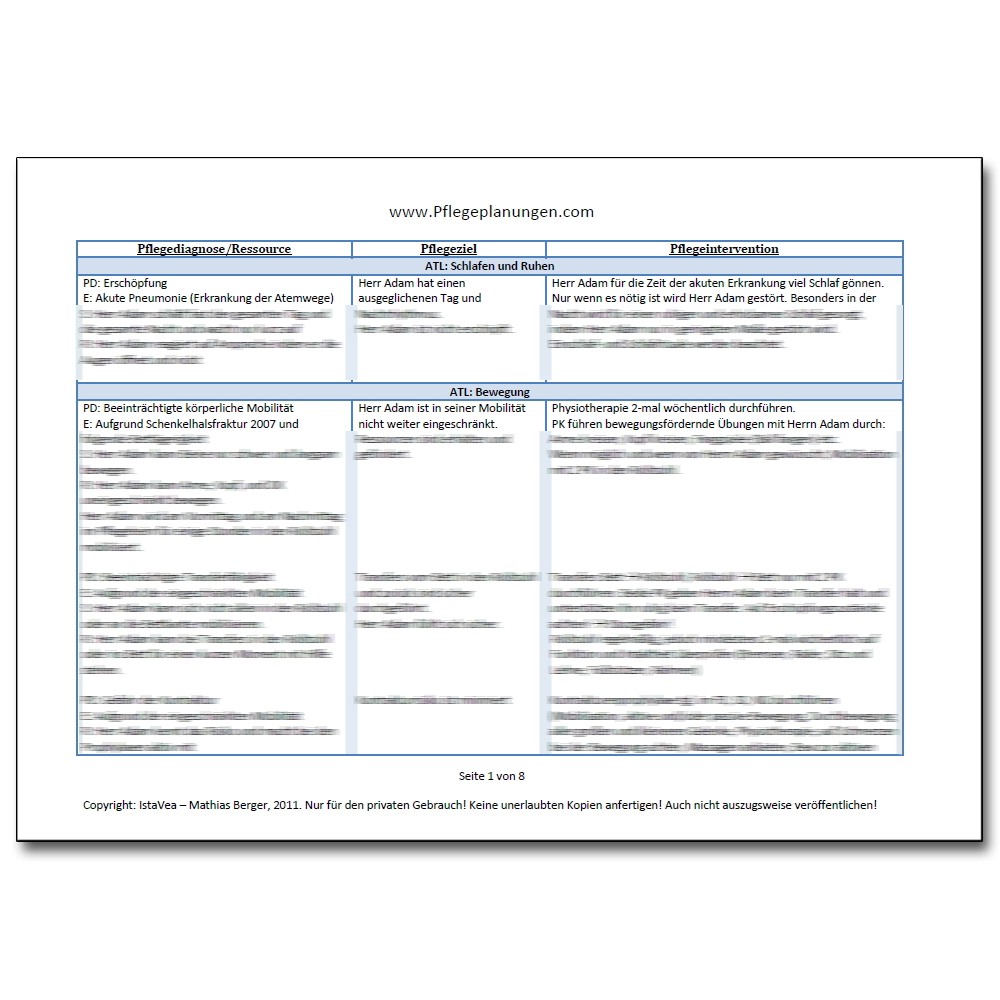
Pesr pflegeplanung muster. Hier finden sie die grundlagen für das schreiben einer pflegeplanung. Anhand des folgenden fallbeispiels soll der in kapitel 4 dargestellte pfle geprozess nach fiechter und meier verdeutlicht und somit das schritt weise vorgehen bei der erstellung einer pflegeplanung exemplarisch dargestellt werden. Individuelle pflegeplanung ip vitalfunktionen 1 soziale interaktion 2 für sicherheit sorgen 3 mobilität 4 sich sauber halten und kleiden 5 essen und trinken 6 ausscheidung 7 sich beschäftigen 8 kommunikation 9 ruhen und schlafen 10 soziale bereiche des lebens sichern 11 hauswirtschaftliche.
Bei der pflegezielklassifikation handelt es sich um ein klassifikationsschema dass die einteilung von pflegezielen in fünf trennscharfen kategorien ermöglicht um das phänomen pflege besser zu verstehen und die umsetzung des pflegeprozesses in die pflegepraxis zu ermöglichen. Herr braun herr braun 78 jahre alt ist vor 2 wochen in ihrer einrichtung einge zogen. Wie genau schreibe ich eine pflegeplanung nach dem pesr format.
Vielleicht hilft ihnen auch die komplette pflegeplanung des herrn weiss mehr und mehr die eigenständigkeit der pflege und ihren anspruch auf eine eigene domäne nachvollziehen zu können. Pflegeplanung vorlage 53 überraschen vorlage traueranzeige für 2019 14 anschreiben beispiele für datenanalytiker vorlage rechnung freiberufler fotos sis pflegeplanung muster 16 bewerbung um arbeitsplatz 15 bewerbung um einen arbeitsplatz muster kostenlos 16 pflegeplanung schreiben muster. Fallbeispiel herr weiss herr anton weiss ehemaliger leidenschaftlicher bibliothekar 76 jahre alt verwitwet 180 zentimeter groß 60 kilogramm schwer.
Ihre methodische pflegeplanungskompetenz und fachliche pflegekompetenz zur erhebung der pflegeanamnese zur ableitung der pflegeprobleme zur festlegung von zur zielerreichung geeigneten pflegemaßnahmen wie in der musterplanung 1 dargestellt ebenso einbringen wie 2. Auflage wurden die transparenzkriterien aktuali siert und in beziehung zur pflegeplanung gesetzt. Hat jemand eine tabelle und kann mir da jemand helfe.
Führen sie die schritte des pflegeprozesses wie in den muster pflegeplanungen durch und vergleichen sie ihre pflegeplanung mit der musterlösung. Pesr schema aedl risikoeinschätzungen und prophylaxen formulierungen ganz neu. Dabei müssen sie nun also 1.
0 0 18 katja lübs schrieb. Qualifikation heilerziehumngspflegerin fachgebiet wohnhaus zitat antwort. Dieses kapitel wird sie schrittweise dazu anleiten.