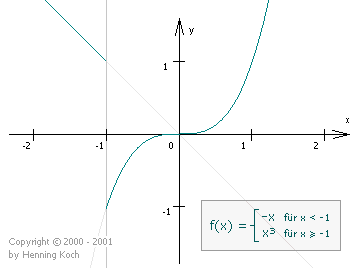← Vertikaler Konzern Beispiel Vergleich Schulden Muster Tunesisch Haekeln Muster →
Eine stelle an der eine funktion unstetig ist bezeichnet man daher auch als unstetigkeitsstelle oder unstetigkeit.
Nicht stetige funktion beispiel. Dafür genügt es ein gegenbeispiel anzugeben also eine funktion die zwar gleichmäßig stetig aber nicht lipschitz stetig ist. F ˇ f ˇ g identifiziert werden. Dass das bild von f in q liegt ist egal da q in r enthalten ist.
Es gibt aber auch unstetige vorgänge wie zum beispiel veränderungen an der börse phasenübergänge oder das verhalten chaotischer systeme wie gewisse wetterphänomene. Nun möchten wir uns noch überlegen dass nicht alle gleichmäßig stetigen funktionen lipschitz stetig sind. Nicht alle gleichmäßig stetigen funktionen sind lipschitz stetig.
Analysis stetigkeit beispiel für eine gleichmäßig aber nicht lipschitz stetige funktion gesucht. Viele vorgänge oder beziehungen zwischen größen in den naturwissenschaften sind stetig. Wenn du allerdings meinst daß eine periodische stetige funktion automatisch gleichmäßig stetig ist dann ist diese vermutung völlig richtig.
Eine 2ˇ periodische stetige funktion kann mit einem element des raums c 2ˇ ff2c ˇ ˇ. Bowery ehemals aktiv dabei seit. Wir könnten das spiel noch weitertreiben indem wir eine funktion suchen die für alle irrationalen zahlen stetig ist und für alle rationalen zahlen nicht aber das muss nicht unbedingt sein da das thema ja eigentlich differenzierbarkeit war.
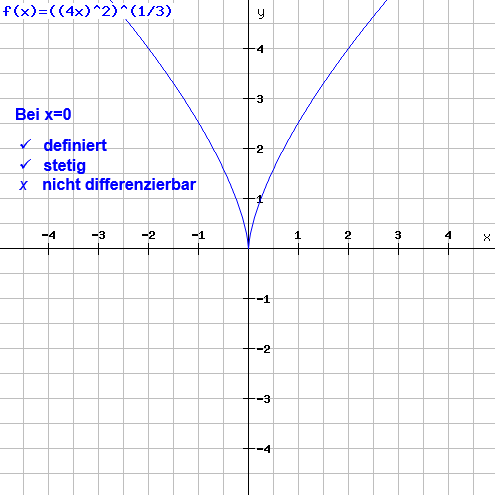
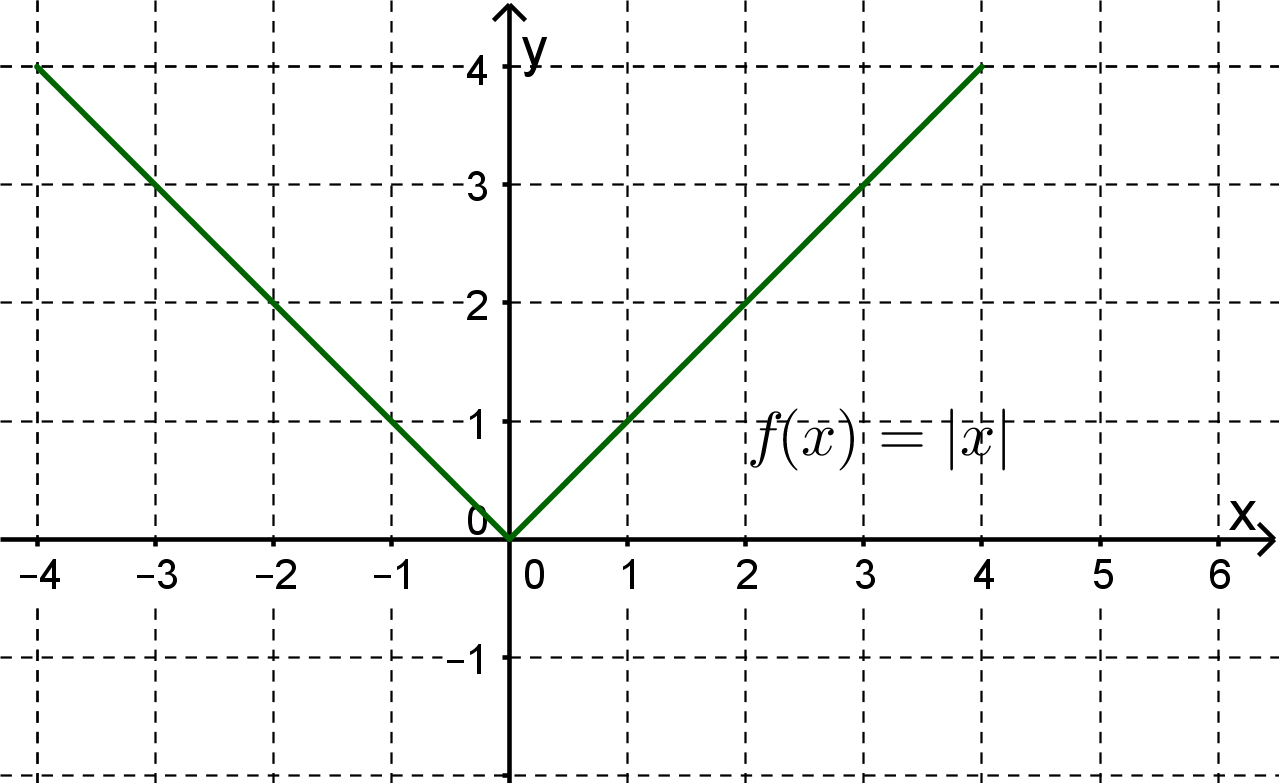
Es gibt keinen grund daß die funktion periodisch sein müßte das ist nicht verlangt. Eine funktion die an jeder stelle ihres definitionsbereichs stetig ist heißt stetige funktion. Das beispiel ist einfach genug und kann kaum überboten werden.
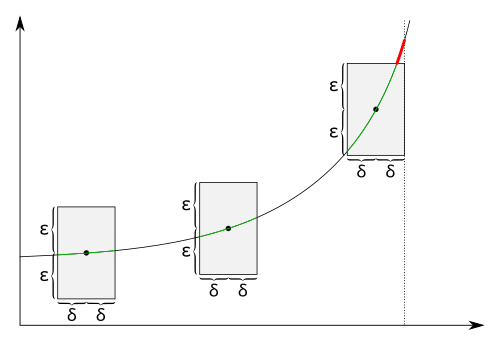
Im artikel stetige funktion wird erklärt wann eine funktion stetig ist und wann sie unstetig ist. Theorem 2 es gibt stetige 2ˇ periodische funktionen deren fourier reihen nicht in jedem punkt konvergieren. Die stetigkeit ist ein wichtiges konzept der topologie.
Die surjektivität der funktion ist ja nicht verlangt. Eine stetige funktion kann charakterisiert werden als eine funktion deren anwendung mit der grenzwertbildung von netzen vertauscht werden kann. Da aber netze im definitionsbereich nicht konvergieren müssen und in der zielmenge netze auch gegen mehrere grenzwerte konvergieren können gilt eine analoge aussage über umkehrfunktionen hier nicht.
In der analysis einem teilgebiet der mathematik wird eine funktion innerhalb ihres definitionsbereichs überall dort als unstetig bezeichnet wo sie nicht stetig ist.