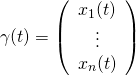← Kuh Basteln Vorlage Kleider Zeichnen Vorlage Lebenslauf Indesign Vorlage →
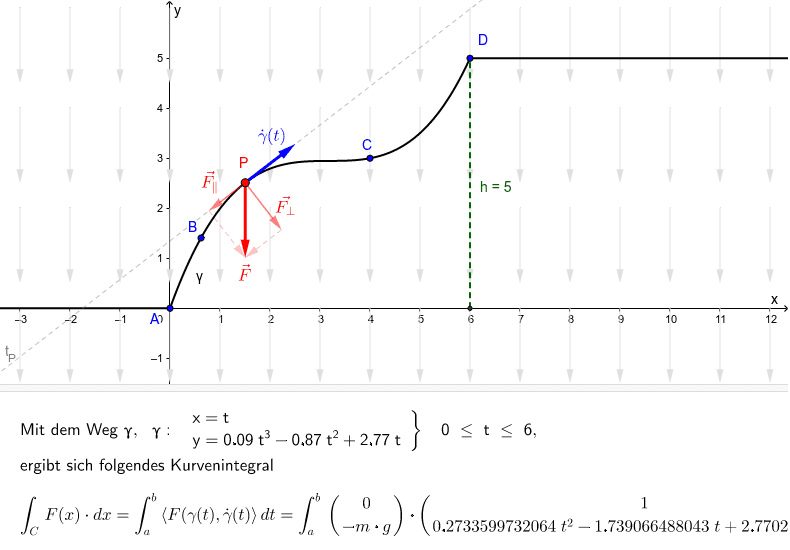
Das eben beschriebene vorgehen mit dem man ein kurvenintegral berechnen kann soll nun an einem beispiel verdeutlicht werden.
Kurvenintegral berechnen beispiel. Die zu integrierende funktion oder allgemein braucht nur entlang der kurve angegeben zu werden ist sie auf definiert so sind bei der integration nur die werte auf der kurve zu berücksichtigen. Kostenlose mathe fragen teilen helfen plattform für schüler studenten mehr infos im video. F ur eine c1 kurve c t von p 1 1 2 nach q 3 5 2 gilt z c f x dx ϕ q ϕ p 9 15 24 interpretiert man f x als elektrisches feld so gibt das kurvenintegral zweiter art die spannung zwischen den beiden punkten pund qan.
ωf ds b af ω t d ω t d t d t. Zu berechnen wir eine normale determinante dabei wird die ableitung vom vektorfeld gebildet beispiel sei v 0 b xy z x y ez 1 c a dann ist rot v e e e x y z. Das vektorfeld f x 2xy z3 x2 3z 3xz2 3y besitzt das potential ϕ x x2y xz3 3yz.
Haben wir eine stetige skalare funktion f und eine mindestens ein mal stetig differenzierbare kurve ω t in parametrisierter form gegeben so berechnet sich das kurvenintegral von f entlang der kurve ω t wie folgt. Ein kurvenintegral oder wegintegral enthält im allgemeinen mehrere variablen ist aber selbst nur 1 dimensional wie die kurve entlang der du integrierst. Hierzu wollen wir das kurven bzw.
Man sollte das kurvenintegral über dem vektorfeld f x y 2xy x x y t entlang des weges ω t t t t von punkt a nach punkt b berechnet werden siehe zeichnung. Der kreis hat die parameterdarstellung x r cos t x r cdot cos t x r cos t und y r sin t y r cdot sin t y r sin t formel 15vs. Kurvenintegral methode wenn g einfach zusammenhängend ist und v die integrabilitätsbedingung erfüllt dann gibt es eine stammfunktion f.
Dies ist ein kurvenintegral erster art der funktion über den kurvenabschnitt der ausdruck ist dabei der allgemein üblichen bezeichnung für die bogenlänge entlehnt s. Linienintegral der funktion entlang des kreises um den ursprung mir radius berechnen. Beispiel wir betrachten die konstante funktion f x y h f x y h f x y h und wollen für diese das kurvenintegral über den kreis mit dem radius r r r um die ursprung berechnen.
Source : pinterest.com